

Summary of the nonlinear sciences by Ben Cheung 9/21/95
Chaos theory is the sciences about non-linearity. Non-linearity is everywhere; the majority of all of nature's phenomena are non-linear. Classically, we've shyed away from non-linearity. We assume a locality of assumption, approximations to convergence, and that small perturbations have no effect globally.
Lorenz first asked is weather deterministic? In 1961 he modeled the weather, and found out that small changes in the input can cause huge changes in the output. The weather is fractal. A small change ripples upward.
Von Neumann proposed a weather prediction machine. Given temperature, pressure, humidity,... It didn't work.
This sensitivity on inputs is known as the butterfly effect. Even if we had an infinitely powerful computer which could measure weather changes 1" apart, we couldn't predict the weather 1 month from now.
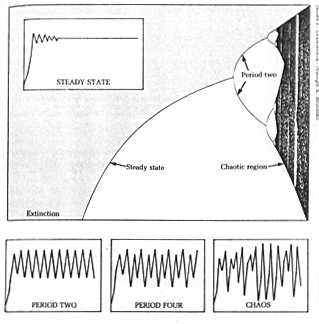
It turns out that non-linear equations result in one of a few basic patterns. They either
(1) Have no steady state and die out.
(2) Have a steady state (1 single solution)
(3) Have 2 solutions (intransitivity)
(4) Have 4 solutions (intransitivity)
(5) Are seemingly chaotic
(6) Have 3 solutions (which implies all the others)
(7) and so forth...
A system driven harder and harder by nonlinearity will
go from 1->2->3->4->5...
![[line]](../Gif.dir/redline2.gif) KEY COMPONENTS TO CHAOS BIFURCATION SOLUTIONS TO DYNAMICAL SYSTEMS
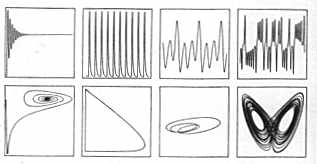
(1) Robert May studied population biologies, modeled w/
x(n+1)=r x(n) * [ 1- x(n) ] <- logistic difference equation
r <= 3 falls to steady state
r > 3 oscillate between 2 val
r = 3.5 oscillate between 4 vals
r > 3.5 chaos
r = 3.8 fractal peg, window of order within chaos
r changes the behavior of this system.
increasing r = drive system harder, increasing nonlinearity
(2) Steve smale - linked topology w/ dynamical systems.
used topology folding. So stability function of maxima/minima of topology
(3) Treat discrete time using a difference eqn.
(4) Yorke = "Period three implies chaos" Proved in a 1D system, if a cycle
of period 3 appears, same system will have regular cycles of all
other bifurcations (2,4,8,7,...) as well as chaotic cycles.
+James Yorke fractal basin boundaries.
(5) The average of the chaos area is higher than the base curve.
(6) Bifurcations faster and faster 4,8,16,32,chaos
(after point of accumulation)
(7) Fractal Peg : Window of order within chaos. Stable cycles suddenly
return even though parameter is rising an odd period like 3 or 7.
Period-doubling bifurcation begins again faster 3,6,12.chaos
7,14,28,chaos
(8) Bifurcation diagram is fractal. When portions are magnified they
turn out to resemble the whole diagram.
(9) Mendelbrot
1. Noah effect: when change happens it is discontinuous,
quick, cascade (change from one attractor to another)
2. Joseph effect :in nature once a stable pt found it tends to
persist. (fixed strange attractor)
(10) Hausdorff-Besicovitch dimension - fractional dimension : describe
fractal embedded structures. Koch Curves, Sierpinski carpets.
(11) Poincare Maps - take a 2D slice of a 3D strange attractor
corresponds to sampling state of a system
every so often, instead of continuously.
KEY COMPONENTS TO CHAOS BIFURCATION SOLUTIONS TO DYNAMICAL SYSTEMS
(1) Robert May studied population biologies, modeled w/
x(n+1)=r x(n) * [ 1- x(n) ] <- logistic difference equation
r <= 3 falls to steady state
r > 3 oscillate between 2 val
r = 3.5 oscillate between 4 vals
r > 3.5 chaos
r = 3.8 fractal peg, window of order within chaos
r changes the behavior of this system.
increasing r = drive system harder, increasing nonlinearity
(2) Steve smale - linked topology w/ dynamical systems.
used topology folding. So stability function of maxima/minima of topology
(3) Treat discrete time using a difference eqn.
(4) Yorke = "Period three implies chaos" Proved in a 1D system, if a cycle
of period 3 appears, same system will have regular cycles of all
other bifurcations (2,4,8,7,...) as well as chaotic cycles.
+James Yorke fractal basin boundaries.
(5) The average of the chaos area is higher than the base curve.
(6) Bifurcations faster and faster 4,8,16,32,chaos
(after point of accumulation)
(7) Fractal Peg : Window of order within chaos. Stable cycles suddenly
return even though parameter is rising an odd period like 3 or 7.
Period-doubling bifurcation begins again faster 3,6,12.chaos
7,14,28,chaos
(8) Bifurcation diagram is fractal. When portions are magnified they
turn out to resemble the whole diagram.
(9) Mendelbrot
1. Noah effect: when change happens it is discontinuous,
quick, cascade (change from one attractor to another)
2. Joseph effect :in nature once a stable pt found it tends to
persist. (fixed strange attractor)
(10) Hausdorff-Besicovitch dimension - fractional dimension : describe
fractal embedded structures. Koch Curves, Sierpinski carpets.
(11) Poincare Maps - take a 2D slice of a 3D strange attractor
corresponds to sampling state of a system
every so often, instead of continuously.
 (12) Intermittency
+Poincare eddies mix w/ regions of smooth flow.
Vorticity is localized. En dissipates only in part of the space.
(13) Phase space - +David Ruelle
phase space a coordinate plot which captures state of system as a point.
So History of system charted by the moving point.
(1) fixed points = steady state
(2) Limit cycles - repeated continuous behavior
(3) Strange attractor - a structured ,layered attractor which never
crosses itself, but represents a system in chaos.
(14) Most systems in nature are iterative, feedback loop.
(15) +Within a particular system could be more than 1 stable solution. Called intransitive.
(16) Universality : Mitchell feigenbaum
+Quadratic difference equation y = r (x - x^2) Feedback loop.
+Feigenbaum found ratio of 1st bifurcation to 2nd , 3rd to 4th,
is a constant rate! 4.6692016090
Tried trigonometric difference equation xt+1 = r sin PI xt
calculated convergence ratio, again 4.669016090
+Universality meant different systems behave identically. a natural
law about systems @ point of transition between orderly and turbulent.
(17) +Lyapunov exponent. Measure of topological qualities corresponding
to unpredictability. Measuring conflicting effects of stretching,
contracting and folding in phase space of an attractor.
Picture of properties which lead to stability/ instability.
Exponent >0 => stretching ;
Exponent <0 => contraction (fixed point attractor) .
Exponent =0 => (limit cycle) Periodic orbit attractor
Strange attractor => w/ at least 1 Exponent > 0
(18) +Energy in natural systems exists on 2 levels: the macroscales,
where everyday objects can be counted and measured, and the
microscales, where countless atoms swing in random motion
+Chaotic / near-chaotic systems bridge gap between macroscales and
microscales. Chaos was creation of information.
+The channel transmitting the information upward is the strage
attractor, magnifying the initial randomness just as the butterfly
effect magnifies small uncertainties into large scale weather
patterns.
(19) +Linear process, w/ nudge tends to remain off track.
+NonLinear process, w/ nudge tends to return to its starting point
(because of strange attractors)
(20) +Entrainment/Mode Locking -- Christian huygens
set of pendulum clocks on a wall swing in perfect chorus line
synchronization! Vibration xmit via wood. One regular cycle
locks into another called entrainment, or modelocking.
Mode locking explains why the moon always faces the earth,
satellites tend to spin in whole-number ratios.
Mode locking in electronics. Radio receiver groups of oscillators,
including biological oscillators. Work in synchronization.
e.g. heart/nerve cells. SE asian firefly blink together.
(21) Scaling.
+D'arcy thompson - macro/micro pattern to living organisms
+Fracticality
(12) Intermittency
+Poincare eddies mix w/ regions of smooth flow.
Vorticity is localized. En dissipates only in part of the space.
(13) Phase space - +David Ruelle
phase space a coordinate plot which captures state of system as a point.
So History of system charted by the moving point.
(1) fixed points = steady state
(2) Limit cycles - repeated continuous behavior
(3) Strange attractor - a structured ,layered attractor which never
crosses itself, but represents a system in chaos.
(14) Most systems in nature are iterative, feedback loop.
(15) +Within a particular system could be more than 1 stable solution. Called intransitive.
(16) Universality : Mitchell feigenbaum
+Quadratic difference equation y = r (x - x^2) Feedback loop.
+Feigenbaum found ratio of 1st bifurcation to 2nd , 3rd to 4th,
is a constant rate! 4.6692016090
Tried trigonometric difference equation xt+1 = r sin PI xt
calculated convergence ratio, again 4.669016090
+Universality meant different systems behave identically. a natural
law about systems @ point of transition between orderly and turbulent.
(17) +Lyapunov exponent. Measure of topological qualities corresponding
to unpredictability. Measuring conflicting effects of stretching,
contracting and folding in phase space of an attractor.
Picture of properties which lead to stability/ instability.
Exponent >0 => stretching ;
Exponent <0 => contraction (fixed point attractor) .
Exponent =0 => (limit cycle) Periodic orbit attractor
Strange attractor => w/ at least 1 Exponent > 0
(18) +Energy in natural systems exists on 2 levels: the macroscales,
where everyday objects can be counted and measured, and the
microscales, where countless atoms swing in random motion
+Chaotic / near-chaotic systems bridge gap between macroscales and
microscales. Chaos was creation of information.
+The channel transmitting the information upward is the strage
attractor, magnifying the initial randomness just as the butterfly
effect magnifies small uncertainties into large scale weather
patterns.
(19) +Linear process, w/ nudge tends to remain off track.
+NonLinear process, w/ nudge tends to return to its starting point
(because of strange attractors)
(20) +Entrainment/Mode Locking -- Christian huygens
set of pendulum clocks on a wall swing in perfect chorus line
synchronization! Vibration xmit via wood. One regular cycle
locks into another called entrainment, or modelocking.
Mode locking explains why the moon always faces the earth,
satellites tend to spin in whole-number ratios.
Mode locking in electronics. Radio receiver groups of oscillators,
including biological oscillators. Work in synchronization.
e.g. heart/nerve cells. SE asian firefly blink together.
(21) Scaling.
+D'arcy thompson - macro/micro pattern to living organisms
+Fracticality
![[line]](../Gif.dir/redline2.gif) EXAMPLES Period-Doubling Cascade Bifurcation in Dynamical Systems
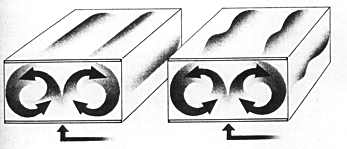
(1) Fluid dynamics. Convection
a fluid cell as it is heated, the center expands because of the
heat, the outside of the fluid cell is cooler and thus sinks.
The expanded center rises. This causes a cylindrical roll
a twin tube (or toroid) of convecting fluid. As the system
is heated further a wobble develops which moves back and
forth. As the heart is turned up just a little more,
a wobble develops on top of the wobble.
+Albert libchaber- liquid helium cell. heat up get Rayleigh-Benard convection
turbulence arrives suddenly
+get convection in cell w/temp diff of 1/1000 degree.
+convection in form of rolls of fluid. Period-doubling cascade appeared.
EXAMPLES Period-Doubling Cascade Bifurcation in Dynamical Systems
(1) Fluid dynamics. Convection
a fluid cell as it is heated, the center expands because of the
heat, the outside of the fluid cell is cooler and thus sinks.
The expanded center rises. This causes a cylindrical roll
a twin tube (or toroid) of convecting fluid. As the system
is heated further a wobble develops which moves back and
forth. As the heart is turned up just a little more,
a wobble develops on top of the wobble.
+Albert libchaber- liquid helium cell. heat up get Rayleigh-Benard convection
turbulence arrives suddenly
+get convection in cell w/temp diff of 1/1000 degree.
+convection in form of rolls of fluid. Period-doubling cascade appeared.
 (2) Current on a disk within a magnetic (B) field,
is a dynamical system. Sometimes reverses direction.
A geodynamo also undergoes this reversing / flipping.
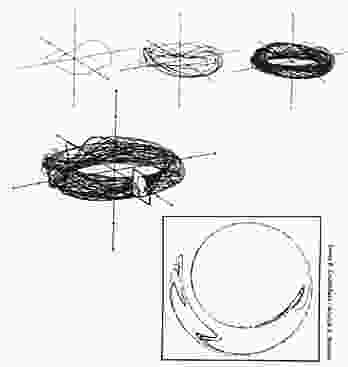
(3) Lorentz modeled a waterwheel with multivariate convection
equation. In phase space this gave the famous
butterly looking Lorenz Attractor.
stable, low-dimensional, nonperiod attractor which never intersects itself.
(4) Oscillators. A swing (can turn erratic as it settles down).
A Pendulum exhibit nonlinear behavior
Pendulum has friction. Phase space = 2 variables: position & velocity
all orbits end at center = position 0, velocity 0. Origin
is fixed point "attracts" the orbits. Spiral inward.
Pendulum w/ spring gets energy; but loses via friction.
Pendulum is driven and damped. A stable orbit is
closed loop in phase space = regular swinging motion e.g. grandfather clock.
System has 2 attractors. A closed loop and a fixed point. Each w/ a "basin"
(5) Red spot on jupiter.
-HI eddies, chaos, swirling hurricanes but red spot immune
-HI coriolis force. Self-organized stable chaos.
(6) Population biology 50mil species w/ limited food,
predator, prey, virus, -> match formula
a population reaches equilibrium, rise, overshoot,fall back.
(7) Mendelbrot studies cotton prices framed in scaling , prices fit!
scaling distribution of cities, game theory ,economics
(8) +Swinnney + Gollub examine enclosed flow between 2 cylinders.
Rotating cylinders produce couette-taylor flow.
First instability a stack of inner tubes flow pattern.
(9) Weather system. Quadratic diff eq w/ low r - stable fixed pt.
static climate , weather same. w/ higher r oscillated between two points.
w/ higher r chaos.
+Lorenz - "almost-intransitive" system :average behavior for long time,
fluctuating wi/bounds. Shifts to different behavior fluctuating but
producing different average.
(10) +AN Kolmogorov and Yasha Sinai
+Dripping faucet. Drip physics. Each drop interrupts light beam.
Records time . As flow rate increased, period-doubling bifurcation.
Drops fall in pairs. Matter of embedding the data in a phase space
of enough dimensions. Fractal dimension, Hausdorff dimension ,
Lyapunov dimension, information dimension
(11) +Chaos in the heart. Normal cardiac regime periodic, nonperiodic pathologies.
Ventricular fibrillation. Ectopic beats, electrical alternans, torsades
de pointes, high grade block escape rhythms, parasystole (atrial
or ventricular, pure or modulated), wenckebach rhythms (simple/complex).
Tachycardia. Fibrillation.
+Aggregate of heart cells from chicken. Saw period doubling , beat patterns
which bifurcated and bifurcated as stimulus applied. Pioncare maps,
intermittency, mode locking.
(12) +Heat diffusion creates instability, surface tension creates stability.
Pull of surface tension makes substance smooth boundaries like the
wall of a soap bubble. Diffusion is mainly a large-scale, macroscopic
process, surface tension is strongest at the microscopic scales.
Laws of pattern formation are universal.
+Snowflakes are nonequilibrium phenomena.
(2) Current on a disk within a magnetic (B) field,
is a dynamical system. Sometimes reverses direction.
A geodynamo also undergoes this reversing / flipping.
(3) Lorentz modeled a waterwheel with multivariate convection
equation. In phase space this gave the famous
butterly looking Lorenz Attractor.
stable, low-dimensional, nonperiod attractor which never intersects itself.
(4) Oscillators. A swing (can turn erratic as it settles down).
A Pendulum exhibit nonlinear behavior
Pendulum has friction. Phase space = 2 variables: position & velocity
all orbits end at center = position 0, velocity 0. Origin
is fixed point "attracts" the orbits. Spiral inward.
Pendulum w/ spring gets energy; but loses via friction.
Pendulum is driven and damped. A stable orbit is
closed loop in phase space = regular swinging motion e.g. grandfather clock.
System has 2 attractors. A closed loop and a fixed point. Each w/ a "basin"
(5) Red spot on jupiter.
-HI eddies, chaos, swirling hurricanes but red spot immune
-HI coriolis force. Self-organized stable chaos.
(6) Population biology 50mil species w/ limited food,
predator, prey, virus, -> match formula
a population reaches equilibrium, rise, overshoot,fall back.
(7) Mendelbrot studies cotton prices framed in scaling , prices fit!
scaling distribution of cities, game theory ,economics
(8) +Swinnney + Gollub examine enclosed flow between 2 cylinders.
Rotating cylinders produce couette-taylor flow.
First instability a stack of inner tubes flow pattern.
(9) Weather system. Quadratic diff eq w/ low r - stable fixed pt.
static climate , weather same. w/ higher r oscillated between two points.
w/ higher r chaos.
+Lorenz - "almost-intransitive" system :average behavior for long time,
fluctuating wi/bounds. Shifts to different behavior fluctuating but
producing different average.
(10) +AN Kolmogorov and Yasha Sinai
+Dripping faucet. Drip physics. Each drop interrupts light beam.
Records time . As flow rate increased, period-doubling bifurcation.
Drops fall in pairs. Matter of embedding the data in a phase space
of enough dimensions. Fractal dimension, Hausdorff dimension ,
Lyapunov dimension, information dimension
(11) +Chaos in the heart. Normal cardiac regime periodic, nonperiodic pathologies.
Ventricular fibrillation. Ectopic beats, electrical alternans, torsades
de pointes, high grade block escape rhythms, parasystole (atrial
or ventricular, pure or modulated), wenckebach rhythms (simple/complex).
Tachycardia. Fibrillation.
+Aggregate of heart cells from chicken. Saw period doubling , beat patterns
which bifurcated and bifurcated as stimulus applied. Pioncare maps,
intermittency, mode locking.
(12) +Heat diffusion creates instability, surface tension creates stability.
Pull of surface tension makes substance smooth boundaries like the
wall of a soap bubble. Diffusion is mainly a large-scale, macroscopic
process, surface tension is strongest at the microscopic scales.
Laws of pattern formation are universal.
+Snowflakes are nonequilibrium phenomena.
![[line]](../Gif.dir/redline2.gif) FRACTICALITY
(1) Coastlines are infinitely long. Fractal
(2) Mendelbrot analyze phone lines, errors line noise intermittent
+Use idea of cantor set "Cantor dust"
+Begin w/ a line remove middle 1/3 remove 1/3 of remaining segments ...
+Cantor set = dust of points that remains, infinitely many
total length is 0. Rather than increase signal strength to drown out noise,
use modest signal accept errors, use redundancy to catch/correct
(3) Dimension 1D,2D,3D. How many dimensions is a ball of twise? From far 0D
From near 3D, from very near 1D, from very very near 3D
Mendelbrot moved beyond dimensions 0,1,2,3... to fractional dimensions
fractals as a way to see infinity . Koch curve, koch snowflake.
Koch curve - triangle add triangle 1/3 size of each side.
Infinite length in finite space. 1.2618D
Peano curves
Sierpinski gaskets - solid 3D triangle cut out center triangle. eiffel tower.
Sierpinski carpet - square cut out 1/9 square. repeat.
Menger sponge = 3D sierpinski carpet, cube. Infinite surface area, zero volume
Fractal = self symmetry self similarity
Hurricane-galactic cyclone, little street twister.
Blood vessels (aorta, capillaries), digestive tract undulations,
lungs bronchal branching-
(4) +1879 Cayley manageable 2nd degree case to intractable 3rd degree case.
3rd degree polynomial x^3-1 = 0
+Given any complex number as a starting point, the question was to see
which of the 3 solutions
newton's method would lead to. It was as if newton's method were a dynamical
system and the 3 solutions were 3 attractors.
+Julia set is a map of roots in complex plane and given starting point which
root will starting pt go to.
FRACTICALITY
(1) Coastlines are infinitely long. Fractal
(2) Mendelbrot analyze phone lines, errors line noise intermittent
+Use idea of cantor set "Cantor dust"
+Begin w/ a line remove middle 1/3 remove 1/3 of remaining segments ...
+Cantor set = dust of points that remains, infinitely many
total length is 0. Rather than increase signal strength to drown out noise,
use modest signal accept errors, use redundancy to catch/correct
(3) Dimension 1D,2D,3D. How many dimensions is a ball of twise? From far 0D
From near 3D, from very near 1D, from very very near 3D
Mendelbrot moved beyond dimensions 0,1,2,3... to fractional dimensions
fractals as a way to see infinity . Koch curve, koch snowflake.
Koch curve - triangle add triangle 1/3 size of each side.
Infinite length in finite space. 1.2618D
Peano curves
Sierpinski gaskets - solid 3D triangle cut out center triangle. eiffel tower.
Sierpinski carpet - square cut out 1/9 square. repeat.
Menger sponge = 3D sierpinski carpet, cube. Infinite surface area, zero volume
Fractal = self symmetry self similarity
Hurricane-galactic cyclone, little street twister.
Blood vessels (aorta, capillaries), digestive tract undulations,
lungs bronchal branching-
(4) +1879 Cayley manageable 2nd degree case to intractable 3rd degree case.
3rd degree polynomial x^3-1 = 0
+Given any complex number as a starting point, the question was to see
which of the 3 solutions
newton's method would lead to. It was as if newton's method were a dynamical
system and the 3 solutions were 3 attractors.
+Julia set is a map of roots in complex plane and given starting point which
root will starting pt go to.